On Setting Thresholds for Counter-based Rowhammer Defenses

An important class of Rowhammer defenses tracks the number of activations a row receives. If this number reaches a Rowhammer threshold, a remedy must be performed to protect the corresponding set of victim rows (an aggressor row affects multiple victim rows). This post describes how to set the Rowhammer threshold as a function of DRAM's MAC value and attenuation factor.
  • MAC is a per-DRAM device metric describing the minimum number of row activations required to mount a single-sided attack.
  • Attenuation is a factor representing the reduction of disturbance errors as the blast radius increases. This factor is assumed to directly corelate with the increase in the number of activations an aggressor row requires to flip bits in victim rows located farther away. For example, an attenuation factor of 10 means that a victim row requires 10 times more activates to flip bits in a victim row located distance 1 from the victim than an adjacent victim (i.e., located distance 0).
  • I am also using the term row distance between two rows A and row B. This is the number of rows between A and B without counting A or B. For example, the row distance between two adjacent rows is 0.
For more on these terms and what they mean, see my Rowhammer terminology cheat sheet. If you need help with Rowhammer, watch my background on DRAM and Rowhammer. Many other videos online provide background on Rowhammer (as an example, check out Prof. Mutlu's lectures).

The main takeaway point is that the Rowhammer threshold must be set to a value much, much lower than the MAC. These schemes track aggressor rows. They do not track victim rows. Defending a victim row against many combinations of aggressor rows (both adjacent and distant) requires setting the Rowhammer threshold very conservatively. To see the final formula, you can skip to the bottom.
Single-sided Rowhammer Attacks
Consider a hypothetical DRAM device whose MAC value is 1024. For our DRAM, a single-sided Rowhammer attack requires 1024 row activations to flip bits. This animated GIF shows K-1 as the aggressor row and K as the victim row. Activating row K-1 1024 times will flip a bit on row K.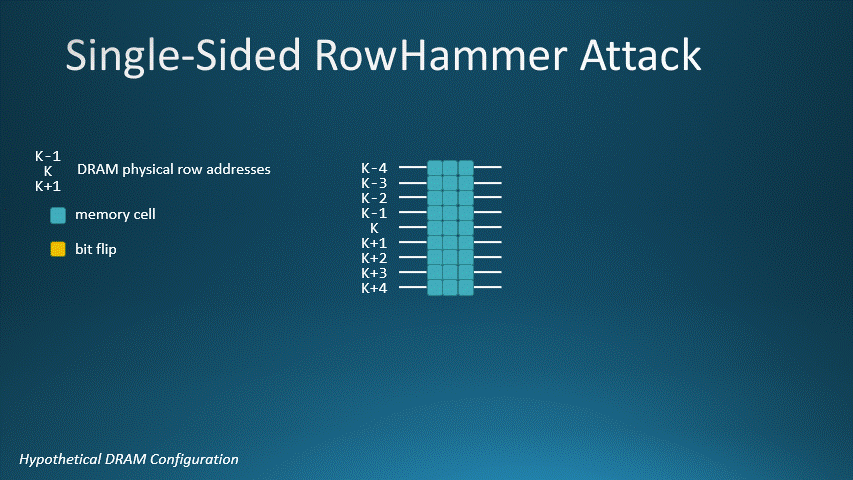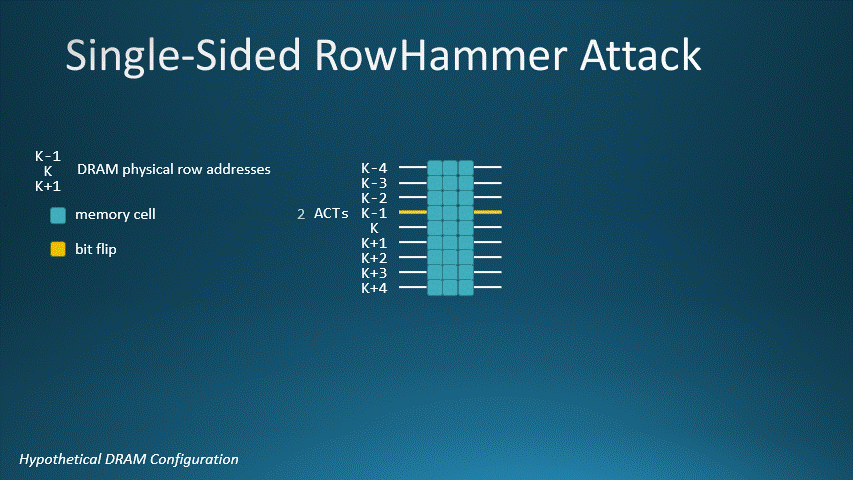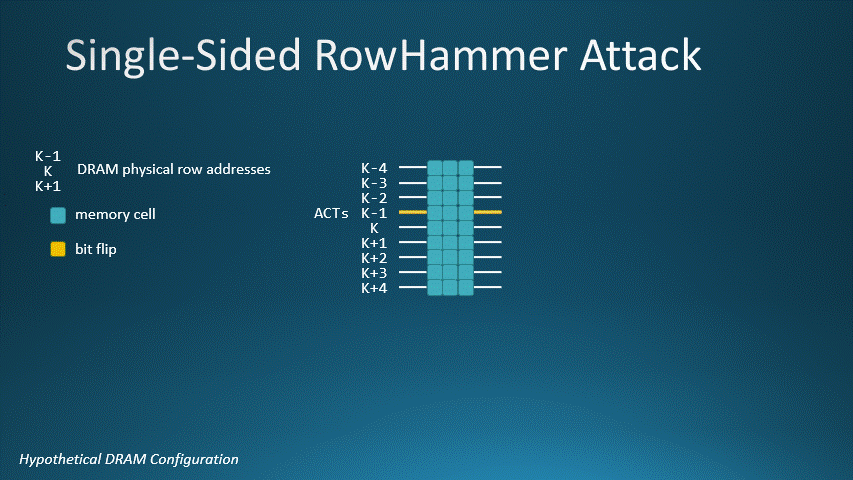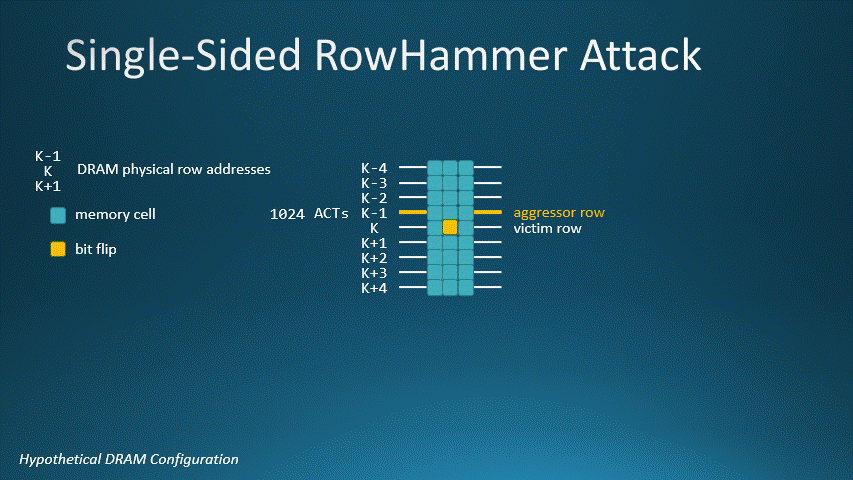
DRAM with MAC=1024, aggressor row K-1 and victim row K. In a single-sided Rowhammer attack, it takes 1024 row activations for K-1 to flip a bit on victim row K.

To stop single-sided Rowhammer attacks, tracking schemes must have a threshold lower than the MAC.

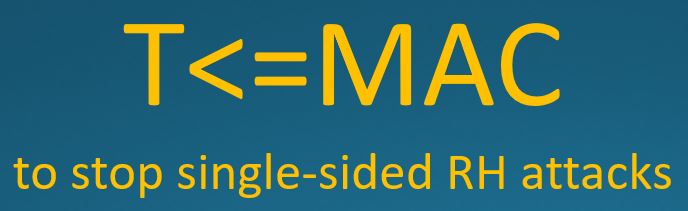
Double-sided Rowhammer Attacks
For our DRAM, a double-sided Rowhammer attack requires 512 row activations to two different aggressor rows adjacent to a victim row. This animated GIF shows K-1 and K+1 as the aggressor rows and K as the victim row. Activating rows K-1 and K+1 512 times will flip a bit on row K.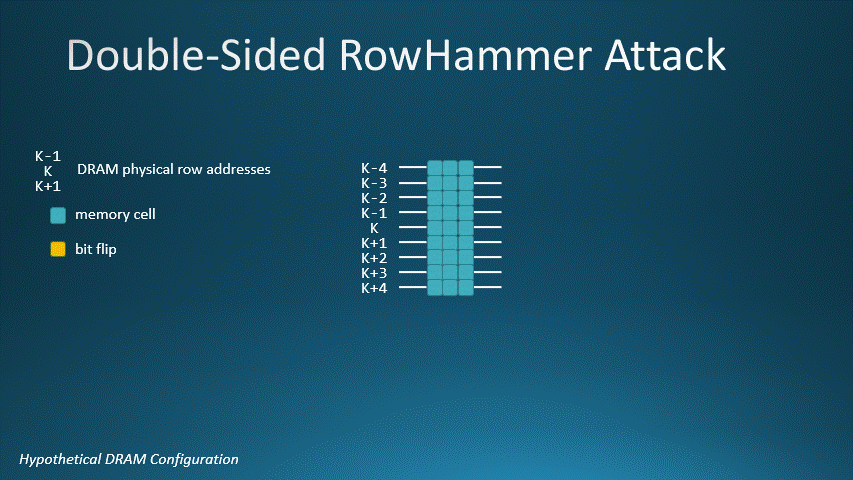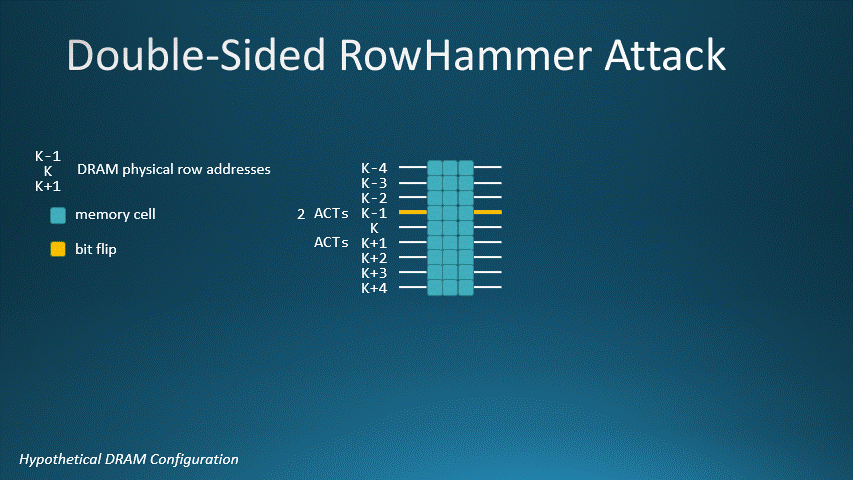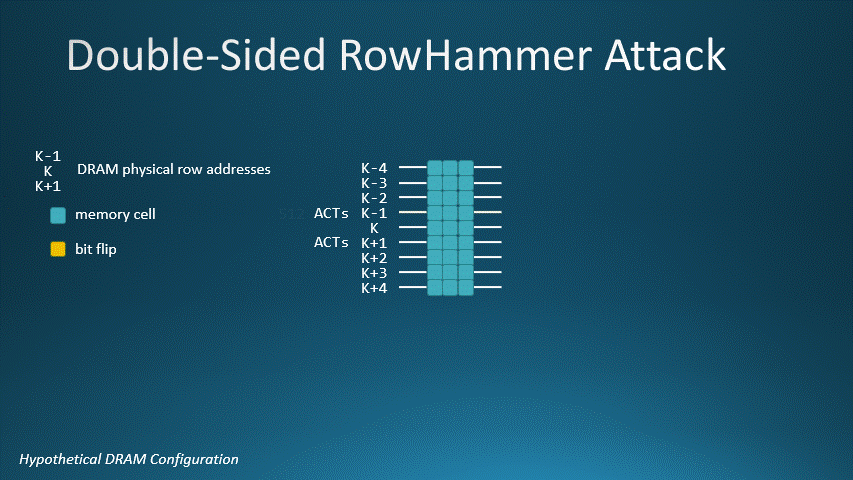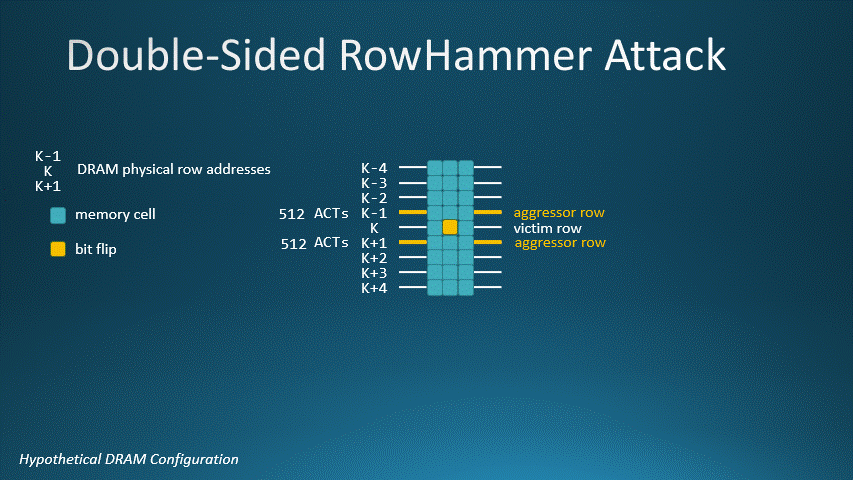
DRAM with MAC=1024, aggressor rows K-1 and K+1, and victim row K. In a double-sided Rowhammer attack, it takes 512 row activations for K-1 and 512 for row K+1 to flip a bit on victim row K.

To stop double-sided Rowhammer attacks, tracking schemes must have a threshold lower than half the MAC value.

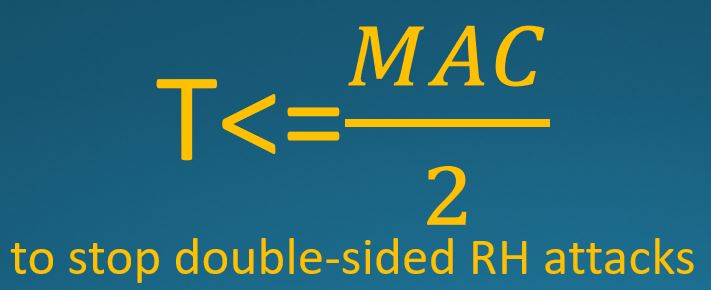
Diffused Rowhammer Attacks
Let's assume that our DRAM has an attenuation factor of 10. Attenuation factor describes the reduction in DRAM disturbance inflicted by an aggressor row to a victim row as the distance between aggressor and victim is increasing. One form of notation for the attenuation factor is RHn:RH1 which denotes the number of row activations needed to flip a bit when the distance between the aggressor and victim rows is n-1. An RH2:RH1 value of 10 means that a distant aggressor row located distance 1 from the victim must be activated 10 times more than an adjacent aggressor row to flip bits . An RH3:RH1 value of 100 means an aggressor row located distance 2 from the victim must be activated 100 times more than an adjacent victim to induce the same "amount of row disturbance".
DRAM with MAC=1024 and attenuation factor of 10. It takes 10240 row activations for aggressor row K-2 to flip a bit on victim row K.


A diffused Rowhammer attack requires more than 3 aggressor rows. For example, let's consider a 4 aggressor row-attack: 511 row activations each to two different aggressor rows adjacent to a victim row and another 10 row activations each to two different aggressor rows located distance 1 from the victim. This animated GIF shows K-1 and K+1 as the adjacent aggressor rows, K-2 and K+2 as the distant aggressor rows, and K as the victim row. An attenuation factor of 10 means that 10 activations of a distant aggressor row are equivalent to an activation to an adjacent aggressor row.
DRAM with MAC=1024, attenuation factor of 10, adjacent aggressor rows K-1 and K+1, distant aggressor rows K-2 and K+2 and victim row K.

To stop diffused Rowhammer attacks in DRAM with a blast radius of 2, tracking schemes must have their thresholds set according to this formula:

For DRAM with arbitrary blast radii, the formula generalizes to:
Further Observations
Note that the threshold needs to be set even lower. The formulae above assume that (1) the tracker is sync-ed with the background DRAM row refresh and (2) every batch of rows that can disturb one another are all refreshed at the same time. Assumption (1) is false when tracking is done by components outside the DRAM device, such as the memory controller or the RCD chip. These components are not sync-ed with the background refresh. Assumption (2) is always false. Instead, one should determine a worst-case bound on the time when any batch of rows is refreshed and compute the maximum number of row activations possible within this worst-case time bound. The threshold must be set lower by this maximum number of row activations.
Acknowledgements
Parts of this analysis were inspired by Graphene , a tracking-based complete RowHammer defense. See section III.D in the paper.
Thanks to Alec Wolman for reading drafts of this.

November 22nd, 2021